【t検定】二つの集団の差を見る検定

2017.08.21
統計学

みなさん、こんにちは。さて、以前【統計学】統計学という心理学研究における最重要技術で「差のたまたま具合」を見るためにはt検定なるものを使うとお話しました。今回はそのt検定を詳しく見ていきましょう。また、今回は統計の基本用語やt検定の用語など詳しく説明していますが、とりあえずExcelでのやり方だけ分かればいいって方はぜひ最後のまとめだけを見ることをお勧めします！t検定の方法まとめ

1. t検定の数式
- 1.1. ＜用語の説明＞
2. t検定とは具体的に何をするものなのか
3. t検定の方法
4. t検定の種類。どのt検定を行うべきか

t検定の数式

統計学は数学によって成り立っています。検定というのは、データの規則性や確率により立てた数式から、目的の情報を判断します。今回のt検定は２つの集団の間の差の情報を目的とします。t検定は必ず2つの集団間でないといけません。二つのテストの点数の差でも、2クラス間の得点の差などとにかく2つの標本間の差を見ます。結論からいくと、t検定の式は

$$t値=\frac{期待値-0}{標準誤差}$$

となります。

＜用語の説明＞

※基本的な用語なので分かる方は飛ばしてもらって構いません。

・t値

t値とはt検定をした際に出てきて、どれだけ差があるのかを示す値です。t値の絶対値が（つまり＋にも－にも）大きければ大きいほど差が確かなことを示します。

・期待値

期待値とは、データの加重平均値のことです。加重とは「重みづけをする」ってことです。例えば、

(1,5,1,4,9,7,5,7,7,2)のような10個の得点のデータがあったとします。各得点が出現する確率はそれぞれ、1は2/10、2は1/10、4は1/10、5は2/10、7は3/10、9は1/10です。加重平均値とは、これらの得点にそれぞれの出現する確立をかけて、全て足し合わせてできた平均値のことなのです。みなさんの知っている平均値は算術平均値といって、$$\frac{1+5+1+4+8+7+5+7+7+2}{10}$$の式で表して、4.8という平均値を算出するものだと思います。そうではなく、加重平均値は、1*2/10+2*1/10+4*1/10+5*2/10+7*3/10+9*1/10の式で表し、4.1という平均値を算出するものです。この平均値を「期待値」というわけです。出現する確率で「重みづけ」されていることが分かると思います。

・標準誤差

標準誤差を算出するための数式は$$標準誤差=\frac{標準偏差}{\sqrt{n}}$$

です。標準偏差とはデータのばらつき具合を表すものです。$${\sqrt{分散}}$$で表すことができます。まあ、分散自体がデータのばらつき具合を表すものなので、当然ってかんじですね。で、サンプル数nのルートで標準偏差を表しているのは、「標準偏差にサンプル数の大きさを反映させるため」です。例えば、5人のみが受けたテストでは、めっちゃできる人ばっかり集まったり、逆に全然できない人ばっかり集まったり、はたまた、天才とおバカがまざっちゃってばらつきが異常に大きくなったりする確率が高くなります。というよりも異常値が出る確率が高くなります。【統計学】オタサーの姫は世界の姫なのか【標本調査】でも言った通り、サンプル数を大きくすることでこういった異常値を回避できるわけです。まとめると

標準誤差は誤差を表す指標です。標準誤差は、標準偏差にサンプル数を反映させたもの。標準偏差（バラツキ）が小さければ標準誤差は小さくなり、またサンプル数が大きければ標準誤差は小さくなる。逆も同様に、標準偏差（バラツキ）が大きければ標準誤差は大きくなり、またサンプル数が小さければ標準誤差が大きくなる。

といった風な理解で完璧です。

t検定とは具体的に何をするものなのか

t検定とは「2標本の差のたまたま具合」を見る、という風に、知能指数と数学のテストの点数の関係という例を使って以前に【統計学】統計学という心理学研究における最重要技術でお話ししたことがありますが、今回は具体的にどのように差のたまたま具合を見るのか検定を行っていきたいと思います。では、以下の例を使って実践していきましょう！

T学校には、AクラスとBクラスがあります。T学校は、新たに開発した数学の指導法の効果を調べるためにAクラスにはその指導法を、Bクラスには従来の指導法を適用しました。そして、数学のテストを行い、両クラスの得点を比較しようとしました。得点の結果は以下の通りです。

両クラスの数学の点数と平均点
出席番号	Aクラス	Bクラス
1	86	75
2	86	67
3	81	63
4	95	40
5	95	57
6	93	37
7	76	40
8	92	73
9	66	89
10	72	75
11	96	41
12	69	71
13	92	53
14	92	42
15	86	90
16	88	84
17	94	90
18	90	30
19	82	65
20	60	48
21	70	89
22	65	66
23	93	59
24	85	57
25	100	33
26	70	73
27	86	34
28	98	60
29	62	82
30	63	53
31	61	34
32	82	59
33	79	82
34	68	80
35	64	41
36	61	42
37	76	48
38	78	65
39	96	42
40	52	71
平均点	80	60

表から、Aクラスでは、平均80点です。そしてBクラスでは平均60点となりました。確かにこの時点んで点数に差は出ていますが、これが本当の差かどうかは検定してみないと何とも言えません。たまたま差が20点出てしまっただけかもしれないからです。そして、この問題を解決するために、t検定を行っていきましょう。

t検定の方法

Excelでt検定を行っていきます。もちろん、検定のための数式は既述した通りにありますが、研究や調査で手計算することはありません。では早速やっていきましょう。

まず、Excelでt検定をするにはツールバーの「データ」へ行きます。そののち、「データ分析」をクリックします。

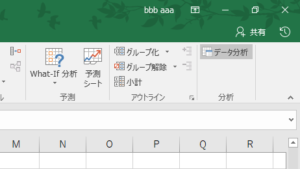
ここから、t検定の項目を探していくのですが、困ったことにt検定の項目は三つあります。抽出した標本別に使うt検定が違ってきますので、以下の説明を見てどのt検定を使うかを確認しましょう。

t検定の種類。どのt検定を行うべきか

・t検定：一対の標本による平均の検定

「一対の標本による」とはつまり「同じ被験者による」ということです。つまり、同じ集団が2つのテストを行ったときなどに使うものです。

・t検定：等分散を仮定した2標本によるt検定

2標本によるっていうのはつまり、2グループの集団がいますよってことです。そして、「等分散を仮定する」とか「等分散を仮定しない」とかの重要性は、「分散（標本のデータのばらつき具合）によって平均値の差の信用度が違ってくる」という認識によります。さきほどの数式を思い出してみましょう。

$$t値=\frac{期待値-0}{標準誤差}$$

$$標準誤差=\frac{標準偏差}{\sqrt{n}}$$

標準偏差とはですから、t値の式を見ても分かるように、分散が変わってくればもちろんt値も変わってきますよね。どう変わるかというと、「標準誤差が大きければt値が小さくなる。t値が小さくなれば差の確かさが無くなっていく。」という感じです。2標本ということは、2つの標本があるわけですよ。2つの標本とも同じ分散だったら、誤差は標本間で少ないでしょう。一方、2つの標本が異なる分散を持つなら誤差はかなり大きくなるため、修正が必要なことが分かると思います。そのため、「2標本の分散が等しいかどうか」というのは非常に大事な要素なのです。そして、もちろん、その修正された式がこのt検定と次のt検定では用意されています。今回はt検定の意味と流れを理解してもらうだけでいいので、そこまでは書きません。